本网讯（通讯员 时尚） 4月26日晚，荷兰乌得勒支大学逻辑教授、哲学逻辑杂志主编Rosalie Lemhoff教授应邀通过网络平台做了主题为“论普遍证明理论中证明系统的存在性”的线上讲座。讲座由beat365官网程勇教授主持，厦门大学哲学系林哲副教授作与谈人。来自国内外的200余名听众参加此次线上讲座。

首先由程勇教授介绍主讲人。Lemhoff教授在数学基础、证明理论等领域作出了杰出贡献。本讲座旨在讨论具有良好性质的证明系统的存在性，Lemhoff教授以序列演算为例讨论中间逻辑中的良好演算的存在性。Lemhoff教授先引入序列演算，再引入良好序列演算的记号定义，最后给出一个可行的判别方法和目前已获得的研究成果。

Lemhoff教授首先介绍了证明论的起源和发展并引出了序列演算。她从希尔伯特在1900年国际数学家大会中提出的23个重要数学问题讲起。其中的第二个问题就是证明算术公理的一致性问题。一致性直观上讲就是自洽，不自相矛盾，即在一个证明系统中不会推演出谬论。这个问题在哥德尔1931年发表的不完全性定理得以解决。虽然结果看似与希尔伯特最初的猜想相违背，但引起了此后证明论的不断衍生和发展。然后她介绍了大家熟悉的自然演绎。自然演绎有许多不同的形式系统，Lemhoff教授介绍了教学中常见的Łukasiewicz第三系统和只有一条公理加分离规则的Meredith公理系统。结构证明论中的主要研究方向之一是证明的正规化问题。所谓一个证明是正规的，是指它中间没有“弯路”，直观上就是证明中没有重复和冗余的部分。Gentzen, Prawitz等人先后分别证明了直觉主义逻辑和经典主义逻辑的正规化定理。Gentzen在证明的过程中发现自然演绎的工具并不方便，于是创建了序列演算。序列演算的美观和易用性使得它成为了普遍证明论和结构证明论中的一种重要证明系统，我们本次讲座也是使用该证明系统。之后Lemhoff教授介绍了经典主义命题逻辑中的序列演算的两条公理：原子公理和矛盾公里；四条结构规则：两个弱化规则和两个收缩规则；对于每一个联结词还有对应的两条操作规则。注意她讨论的序列演算         的两边是公式集，所以我们无须考虑它们的顺序问题，于是结构规则中便不需要有交换规则。G1_{cp}是包含合取析取蕴含的序列演算的逻辑系统，可以证明它在CPC中是可靠完备的，即其中可证的定理在CPC中都是有效式。类似的对于G1_{ip}在直觉主义逻辑中也是可靠完备的。直觉主义序列演算要求序列的右边Δ集合至多含有一个公式。教授随即举出了G1_{cp}中可证的公式          并指出它在G1_{ip}中并不可证。

在讲座的第二部分，Lemhoff教授主要介绍了多种逻辑系统下的序列演算和一些重要定理。首先Lemhoff教授引入模态逻辑的概念，即在逻辑形式语言中引入模态操作符Œ。模态逻辑符在哲学、计算机、数学等领域都是一个重要的研究对象。Lemhoff教授重点讨论了G1和G3系统，它们的区别在于G3没有结构规则但是扩展了它的公理达到与G1+Cut的等价性。Cut规则是符合人们通常数学证明直观的规则，即通过证明引理来证明目标定理。因为结构规则和Cut规则的存在使得G1不像G3一样拥有一些很好的性质，比如演绎的子公式特征、证明检索的可终止性。于是我们很自然地想到消去Cut的使用，教授说明了消去Cut规则会使得证明的体量显著增大。

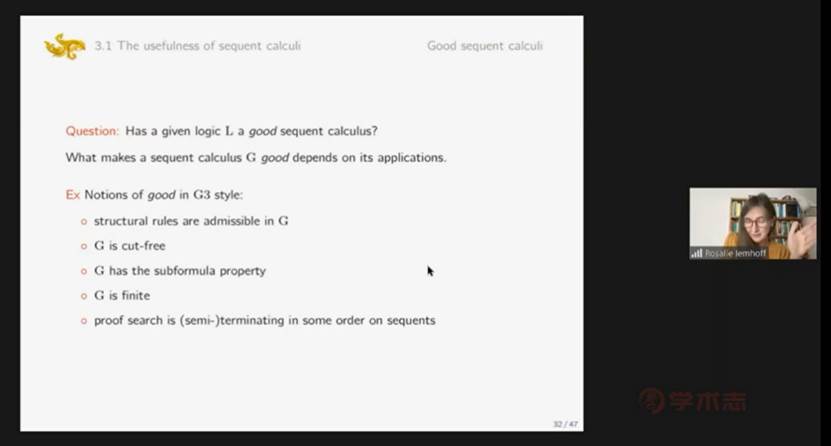
第三部分是序列演算的存在性。Lemhoff教授的报告十分详尽，她介绍了存在性的起源发展和当今研究现状，也介绍了许多积极的研究成果。虽然我们可以对所有逻辑系统定义出它的序列演算，但并不具有良好的、像G3那样的、可用于计算的性质。于是Lemhoff教授参照G3给出了一个序列演算是良好的定义。之后Lemhoff教授进一步阐述了良好序列演算的概念并在一些逻辑系统中讨论该良好序列演算的存在性。比如模态逻辑、中间逻辑、条件逻辑等都具备良好的序列演算。但证明一个逻辑系统不具备良好的序列演算并不是一个平凡的过程。我们采取的通用方法是对于一个逻辑类找到其中一个良好演算的必要性质P，在证明其一个子类不具备该性质从而证明该子类不具备良好演算。但P的选取并非一个容易的过程，选取过强或过弱都会带来一些困难。Lemhoff以中间逻辑为例，选取的性质P是一致插值UIP并给出了证明该性质的方法。此处插值是指对于一个演绎           可以找到一个公式            使得         且

。通过一致插值性质可以证明中间逻辑中仅有7个逻辑具有良好的演算，即IPC,Sm,Gsc,LC,KC,Bd2,CPC，而例如S4,K4系统并没有这样的性质，即使它们存在一些很好的演算但并没有达到我们需要的计算标准。

在评论环节，首先由林哲副教授进行简短的评论，并提问如果不是限制在G4中而是更为自由的序列演算如标号演算以上的结果是否仍然成立。Lemhoff教授指出所介绍的方法是通用的，但在例如标号演算中证明UIP性质可能会变得比较困难。接着林哲副教授指出除了UIP之外的性质，比如cut-elimination等会依赖于演算的形式所以良好演绎的记号会发生变化。程勇教授接着提问UIP是否是良好演算的充分条件，Lemhoff教授认为可能并非如此，这是一个值得研究并且她正在研究的问题。学术志参会者和会议其他参会者也与Lemhoff进行了详细深刻的交流。

最后，程勇教授对本场讲座进行了总结，并对Lemhoff教授带来的精彩讲座表示了感谢。

（编辑:邓莉萍  审稿：刘慧）